Participating at informatiCup 2021

Last Thursday, the final round of the informatiCup 2021 took place. Our team placed third of all 30 participating teams and received the GitHub special award!

In this blog post, I would like to outline the technical aspects of our solution as well as look at what are able to away from working on this project for an extended amount of time.

The challenge

From October until January, three friends and I participated in the 2021 informatiCup. The informatiCup is a computer science competition for college students held by the German Informatics Society. It is designed to be an all-around computer science competition: To succeed, the teams need solid theoretical approaches as well as programming and project management skills.

This year’s challenge was about the game spe_ed. The rules are as follows:

spe_ed is a multiplayer, online, turn-based game where all players move at once. There are 2-6 players in each game.
The players move in cells. Each player has a position, speed and direction.
Each round, every player is given all information about the players and the board. The player has to send their action to the server before a deadline expires, usually 8-12 seconds.
Each round, every player chooses between the actions change_nothing, turn_left, turn_right, speed_up, speed_down. The maximum speed is 10, the minimum speed is 2.
Every player leaves a trace that does not vanish throughout the game.
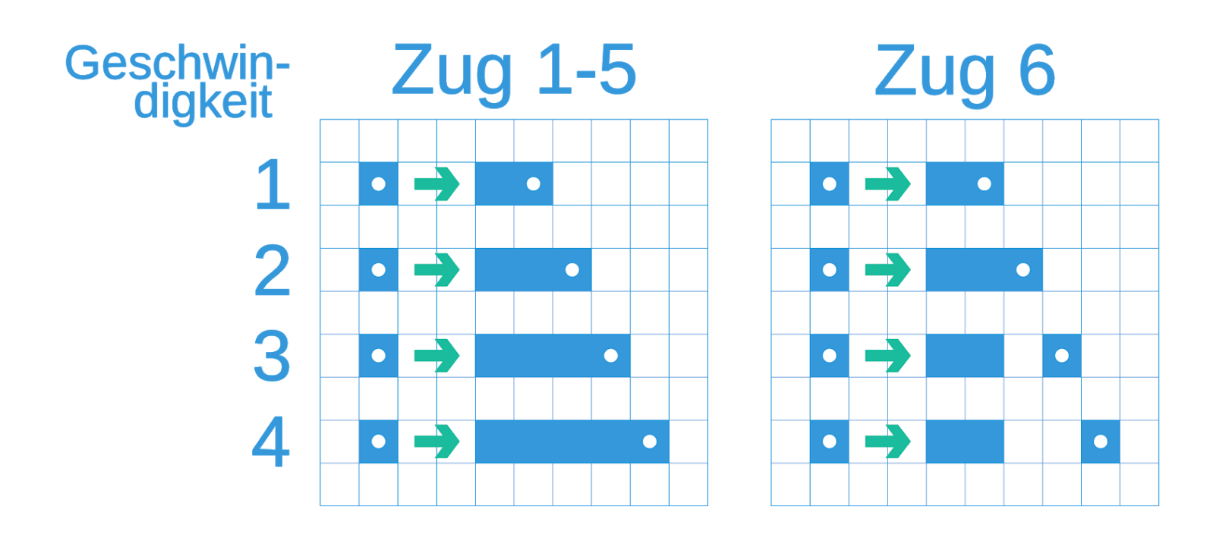
Every sixth round, the players can jump. A player jumps when their speed is 3 or higher, they leave a hole of (speed - 2) as illustrated below.
The deadline and board dimensions are unknown before the game.
When a player collides with another player, a trace or a wall, they lose.
The last surviving player wins.

image illustrating the jumping mechanics

One thing to note about spe_ed is that one game could take multiple hours as there are often over 500 turns, each with a deadline of about 10 seconds. Therefore, we created a script to visualize past games.

One game looked like this:

Getting started

In October, we decided to look into the challenge, what could go wrong?

First of all, we brainstormed possible ways to solve the challenge. We thought that game theory and Reinforcement Learning were two promising approaches, so two of use spent time getting to know these strategies.

While working them concurrently, the Reinforcement Learning team tried various things, but a few problems persisted:

A large, but discrete state space. Using lookup tables is not economical because of the \(2^{n^2}\) possible board states, where \(n\) is the width of a quadratic window of the board (This calculation even excludes player positions, speeds and directions).
The reward function. A player should be trained to win in the long run, but the games can last 500 turns. Designing a working reward function is hard.

Instead, we got good results using a well-known approach from game theory.

The MiniMax algorithm

After re-creating the game environment, the game theory team got good results with a simple MiniMax algorithm. With MiniMax, a full game tree is created. Each node gets a score. The leaves receive their scores through the use of a heuristic. The inner nodes’ scores are calculated based on their children’s scores. It is assumed that the enemy players always try to minimize the scores whereas our own player maximizes the score. In the end, the action with the highest score is used.

Implementing the algorithm was not hard, but finding an appropriate heuristic even more so. We wanted something that was fast to calculate (it has to be executed for every leaf) but also represents the board state well. At the end, we went with the number of degrees of freedom that a given player has, in other words, the number of actions a player can execute without dying.

There was one problem with this strategy: Low search depth. As there are five actions that each player can execute each round, the game tree grows quickly in size. Therefore, the MiniMax algorithm can only see 7-10 rounds ahead, whereas a game might have 500.

We tried optimizing the algorithm with alpha-beta pruning and increased our search depth by a few turns, but it was clear that an exhaustive search would not work for long-term planning.

Random methods

Next, we tried using Monte-Carlo tree search with spe_ed but quickly realized it would not work since the algorithm assumes everone to move sequentially, but in spe_ed, everyone moves at the same time. Instead, we tried just using monte-carlo sampling (we called a single sample “rollout”). One rollout uses random actions until no actions can be performed anymore. It is often possible to perform a could hundred thousand rollouts before the deadline. A basic approach is to look at the longest paths and choose the action that yields the longest paths.

This approach yielded very good long-term planning, but completely ignored the interaction with other players. To fix that, we had to look at what our opponents could be doing in the next time.

Probability tables

Since we never know what exactly our enemies will do next, we assume that they will choose uniformly between all available actions. With this assumption, we look at the next turns and assign probabilities to each board cell. The higher the values, the higher the probability that the cell will be filled at some point in the future.

This is a heatmap of how such probability tables look after a couple of iterations (the blue cells are players, grey cells are already filled, we don’t calculate probabilities for ourselves):

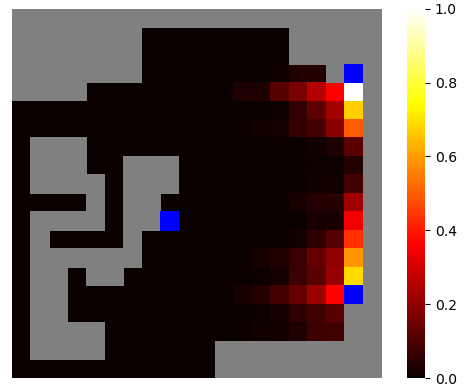
heatmap of the probability tables in action

These maps contain all information about our enemies; the last step is to combine them with the rollout data.

Combining the strategies

Every strategy I described has its strengths and weaknesses. Therefore, we combined them into one solution.

It basically boils down to this:

We always use rollouts to evaluate our situation.
If enemies are near, we also calculate probability tables.
If enemies are very near, we use the MiniMax algorithm with them as the minimizer.
We only use actions on which MiniMax, if used, yielded good scores.
For each path with a length above a certain cutoff, we determine the average probability score along the way.
For our final decision, we try to maximize the number of long paths starting with the taken action; but we also want to minimize the average path probability.

This combination of strategy gives us perfect playing for a few rounds (MiniMax), good long-term planning (rollouts), also with respect to enemy players (probability tables).

Our implementation

We implemented this strategy using the programming language Go. The main reason for this was concurrency and performance, as the number of performed rollouts has a large impact on the desicion quality of the algorithm. The choice programming language delivered: We never really had to struggle with performance and prototyping was pretty fast as well!

It turned out that since we did not tell our bot how to behave except to stay away from enemies, it performed very well against most enemy teams, winning more than \(\frac{2}{3}\) of the games against all teams but one, losing one or more games against only \(8\) of them (even though approximately \(30\) submitted a paper in the end).

What did we learn?

Even though we placed third, it still showed that we are all first year’s bachelor’s students, especially in comparison with the teams that are almost done with their master’s thesis.

One key takeaway for me is that it’s never a waste to focus on tooling when starting out on a project. While we did develop logging for full games, GUIs for running games and more, the lack thereof did slow us down in the first place. We would have also profited from more visualization, especially while developing the rollouts or probability tables. Also, more reproducible test scenarios would have helped to assess whether a code change actually improved our program’s behavior.

Another takeaway for me is that prototyping strategies for problems where there is no clear solution is essential. These prototypes have to be far from perfect, they just have to answer the question “could this approach work in principal?”.

I also think that I will profit from more lectures on math and theoretical computer science as the ability to formalize and think abstractly about problems helps a ton while deciding how to tackle them.

Attribution

The informatiCup logo and rules explanation graphics were taken from https://github.com/InformatiCup/InformatiCup2021.

The Go gopher was designed by Renee French. http://reneefrench.blogspot.com/