Going Quantum
Last weekend, I was able to participate at iQuHACK 2021, the interdisciplinary Quantum HACKathon. iQuHACK is an annual hackathon organized by MIT. Unlike last year, this year’s event was entirely online so it was open to international participants, many of which in different timezones. With two peers from Hasso-Plattner-Institut, we devoted our weekend to learning about the state of quantum computing and its possibilities.
At iQuHACK, there were three divisions:
- Quantum Annealing. This was the division we participated in. The hardware was provided by D-Wave and conveniently accessed with the Ocean SDK.
- Gate-based. This division used universal quantum hardware consisting of gates that manipulate the qubits. The hardware was provided by IonQ.
- Hybrid. This division sought to combine quantum annealing with the gate-based model.
What is Quantum Computing in general?
Quantum Computing tries to use phenomena that occur at very small scales (quantum scales) for computing. Unlike classical computers which use voltages to represent the boolean values 0 and 1, quantum computers use qubits that can be in states between 0 and 1. These states are called superpositions of 0 and 1. When you measure a qubit, their superposition determines the probability of them being measured as 0 or 1.
The real power of qubits comes from a property called entanglement. This means that two or more qubits have interacted in a way that their states cannot be described independently anymore. Just like multiple voltages are combined to bytes, one can combine multiple qubits to describe a larger state space.
Different states of a quantum system contain different amounts of energy. This is what is called the energy landscape of the system. Usually, a system will tend to change towards a local energy minimum.
What is Quantum Annealing?
Quantum Annealing is a special algorithm to implement an adiabatic quantum computer. The “adiabatic” comes from the adiabatic theorem of quantum computing . The theorem says that if a change on a quantum system is acting slow enough, the system will stay in the state of minimal energy.
To put it concretely, if we put the system in a global energy minimum with a known energy landscape and slowly change that landscape, the system will end up in the global minimum of the second landscape. To solve a problem with quantum annealing, we need to design an energy function (Hamiltonian) which is minimal when the system state is a solution.
In contrast, gate-based quantum computing uses quantum logic gates similar to classical electron logic gates to manipulate a quantum state. It then measures and records the qubits to obtain a solution. This process is of inherently discrete nature (the qubits go through one gate at a time) whereas a quantum annealer works in an analog way.
These two approaches to quantum computing have shown to be polynomially equivalent, but they each have advantages and disadvantages: Quantum annealers are not universal, i.e. they are not able to perform Shor’s algorithm, for example. Still, they are able to solve certain types of problems very well, even with large amounts of variables. Gate-based quantum computers are universal but still have issues integrating more qubits and reducing noise.
How do you formulate problems for D-Wave systems?
General problem formulation
The primary programming model used is that of a Binary Quadratic Model (BQM). The term binary means that a variable has two possible values. The values used determine th variant of the BQM used. This model comes in two variants: Ising (values -1 and 1) and Quadratic Unconstrained Binary Optimization (QUBO, values 0 and 1) which I talk about here. To create the energy function that will be minimized by the quantum annealer, a bias term is introduced for every variable. Also, couplings between two qubits can be introduced.
If \(x_1\) and \(x_2\) are the binary variables, \(a\) and \(b\) the biases, \(c\) is the coupling term and \(d\) is a constant, the energy of the system would be represented as
$$E = ax_1 + bx_2 + cx_1x_2 + d$$
A nice metaphor for the model: Imaging having to decide which members of a sports team should play in a certain match. There are stronger and weaker players (bias term). Also, there are combinations of two players that boost the team (positive coupling) or weaken the team (negative coupling).
A table for the values of E in terms of \(x_1\) and \(x_2\) would look like this:
| \(x_1\) | \(x_2\) | \(E\) |
|---|---|---|
| 0 | 0 | \(d\) |
| 0 | 1 | \(b+d\) |
| 1 | 0 | \(a+d\) |
| 1 | 1 | \(a+b+c+d\) |
If you have set values for \(E(x_1, x_2)\), it is possible to determine your coefficients \(a,b,c,d\) by solving the linear system of equations. That way, you can implement basic logic operations, e.g. AND, OR, XOR etc. From there, implementing a one-hot encoding with additional variables requires a bit of algebra but is no rocket science. When you have your coefficients, you can give them to a D-Wave Sampler which tries to find the energy minimum.
Our Project
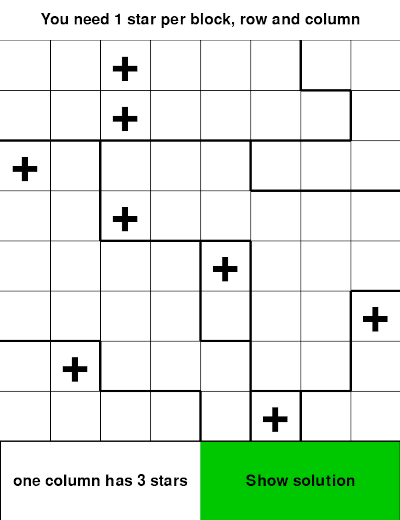
For the hackathon, we accepted a D-Wave challenge. The challenge was about the puzzle Star Battle / Two Not Touch by Krazydad. You can find his intro to the puzzle here.
First, we had to decide on how to encode possible solutions. Since every cell of the board could either contain a star or be empty, one binary variable for each cell was appropriate.
Second, we had to think about the thing we are trying to minimize. For a problem like the Travelling salesman problem, this would be the distance travelled. Since we did not want to minimize anything but instead comply with all constraints, we moved on to the next step.
Third, we needed to find all constraints and encode them into the QUBO.
- Each block, row and column needs to contain the specified number of stars. This could be done with truth tables and algebra, but we used a D-Wave helper function provided with the Ocean SDK.
- No blocks are allowed to be adjacent. For this constraint, the energy should be minimal if there is at most one star in two adjacent cells. It should be higher when there are two stars in two adjacent cells.
We added constraint 1 for every row, block and column to our model and constraint 2 for every pair of adjacent stars.
Results
Our program was able to solve puzzles of easy and medium difficulty correctly 100% of the time and puzzles of hard difficulty 90% of the time. We were very satisfied with the results as we didn’t expect a system with 196 variables system to work as well.
Creating a nice user interface
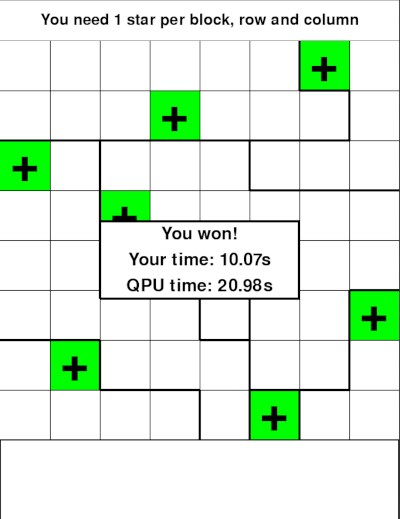
Additional to just implementing a solver, we created an interactive user interface so everyone (with a D-Wave Leap API token) could play against the quantum computer. Here are some screenshots of our UI:
Documentation
Our GitHub repository is available under here. It contains a detailed README as well as final presentation slides that explain further how our solver works.
Conclusion
Overall, I had a great experience at iQuHACK 2021. I learned a lot about the possibilities and challenges of quantum computing.